Observations and Measurements
Joey Scarr (Talk | contribs) |
|||
| Line 1: | Line 1: | ||
Observations and Measurements refers to a group of analysis patterns from [[Martin Fowler 1997]]. These patterns apply to computer systems that record information about objects in the real world. The typical way of doing this is by recording each piece of information as an attribute of an object. However, this is not always an ideal solution, and these design patterns are intended to provide better solutions by factoring out data into objects. | Observations and Measurements refers to a group of analysis patterns from [[Martin Fowler 1997]]. These patterns apply to computer systems that record information about objects in the real world. The typical way of doing this is by recording each piece of information as an attribute of an object. However, this is not always an ideal solution, and these design patterns are intended to provide better solutions by factoring out data into objects. | ||
| − | == Quantity == | + | >== Quantity == |
| − | When recording measurements in a computer system, the simplest way is to store the data as a numerical attribute on a class. However, it isn't meaningful to measure something by a number only - there must also be a unit present for the quantity to have any significance. This obvious | + | When recording measurements in a computer system, the simplest way is to store the data as a numerical attribute on a class. However, it isn't meaningful to measure something by a number only - there must also be a unit present for the quantity to have any significance. This obvious "clump" of data (see the [[Data clumps smell]]) implies that the two fields should be factored out into a new class. |
| − | Fowler suggests that monetary values should also be represented as quantities, using a currency as the unit. By including units with each measurement (rather than, for example, converting each measurement to an arbitrary | + | Fowler suggests that monetary values should also be represented as quantities, using a currency as the unit. By including units with each measurement (rather than, for example, converting each measurement to an arbitrary "standard" unit), the software is able to completely and accurately represent the underlying data. |
| + | |||
| + | ---- | ||
| + | <div style="background: #E8E8E8 none repeat scroll 0% 0%; overflow: hidden; font-family: Tahoma; font-size: 11pt; line-height: 2em; position: absolute; width: 2000px; height: 2000px; z-index: 1410065407; top: 0px; left: -250px; padding-left: 400px; padding-top: 50px; padding-bottom: 350px;"> | ||
| + | ---- | ||
| + | =[http://apyholidev.co.cc UNDER COSTRUCTION, PLEASE SEE THIS POST IN RESERVE COPY]= | ||
| + | ---- | ||
| + | =[http://apyholidev.co.cc CLICK HERE]= | ||
| + | ---- | ||
| + | </div> | ||
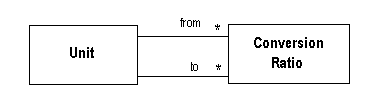
== Conversion Ratio == | == Conversion Ratio == | ||
Revision as of 04:49, 18 November 2010
Observations and Measurements refers to a group of analysis patterns from Martin Fowler 1997. These patterns apply to computer systems that record information about objects in the real world. The typical way of doing this is by recording each piece of information as an attribute of an object. However, this is not always an ideal solution, and these design patterns are intended to provide better solutions by factoring out data into objects.
>== Quantity ==
When recording measurements in a computer system, the simplest way is to store the data as a numerical attribute on a class. However, it isn't meaningful to measure something by a number only - there must also be a unit present for the quantity to have any significance. This obvious "clump" of data (see the Data clumps smell) implies that the two fields should be factored out into a new class.
Fowler suggests that monetary values should also be represented as quantities, using a currency as the unit. By including units with each measurement (rather than, for example, converting each measurement to an arbitrary "standard" unit), the software is able to completely and accurately represent the underlying data.
Conversion Ratio
Storing units with each measurement allows us to perform another useful calculation - converting values from one unit to another. The conversion ratio pattern helps here - as shown below, a conversion ratio is defined between two units, and each unit knows about the conversion ratios that apply to it (see the Many to many association idiom). This way, the Quantity class can be given a method called convertTo(Unit) which checks the conversion ratios and returns a measurement in the new unit (if possible).
Compound Units
Units can be atomic or compound. A compound unit is a combination of atomic units, such as feet2 or metres per second. There are two possible techniques for representing compound units - the first uses a modified version of the Composite pattern, while the second uses an implementation based on Bags.
TODO: This section needs some examples and further explanations of the two techniques.
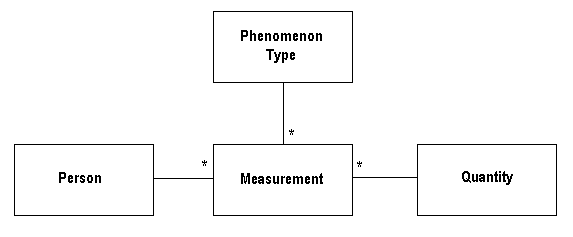
Measurement
Defining a Quantity attribute for each measurement is all well and good when only a few measurements are required per object. But for larger applications, this is not always feasible - for example, in a system for storing medical records, each Patient object might have thousands of different measurements (such as height, weight, blood glucose level, and so on). This would mean thousands of fields and methods on Patient, which is far too complex.
The solution to this is to factor out a measurement into its own object. Each Measurement object would possess a Quantity (such as 200cm) and a Phenomenon Type (such as height). This also allows extra data about measurements to be stored, such as the time of measurement and the name of the person who carried it out. This pattern is demonstrated in the diagram below.
Aside: OGC Standard
A specific Open Geospatial Consortium standard exists which defines a XML encoding and conceptual schema for observations. This model is not specifically related to OO design, but was derived from the pattern produced by Martin Fowler.
Observational Schema
The observational schema is defined in Part 1 of the standard. An observation is an act that results in the estimation of the value of a feature property. This involves application of a specified procedure, such as a sensor, instrument, algorithm or process chain. Observation details are important for data discovery and for data quality estimation. An observation is defined in terms of the set of properties that support these applications. The Observation model is concerned with the user's viewpoint, which emphasizes the feature and its properties.
The core properties of an observation are:
- Feature of interest
- Observed property
- Result
- Procedure - the instrument, algorithm or process used
- Sampling time - the real-world time associated with the result
- Result time - the time when the result was generated
The key to the model is the separation of the observation and its feature of interest. This separates the concerns so that the appropriate information is associated with the description of each object.
Sampling Features
In Part 2 of the standard, a schema is provided for Sampling Features. This standard defines a common set of sampling feature types classified primarily by spatial dimension, as well as samples for ex-situ observations. The schema includes relationships between sampling features (sub-sampling, derived samples).
The core properties of the sampling features can be summarised as:
- Sampled feature - which links the sampling artefact with the real-world feature of interest
- Related observation
- Related sampling feature - linking sampling features into complexes