User:Jenny Harlow/Design study/Final design detail

Sequences

I do not discuss the design patterns used here in detail where these have already been covered in the initial design detail.

Main types and classes

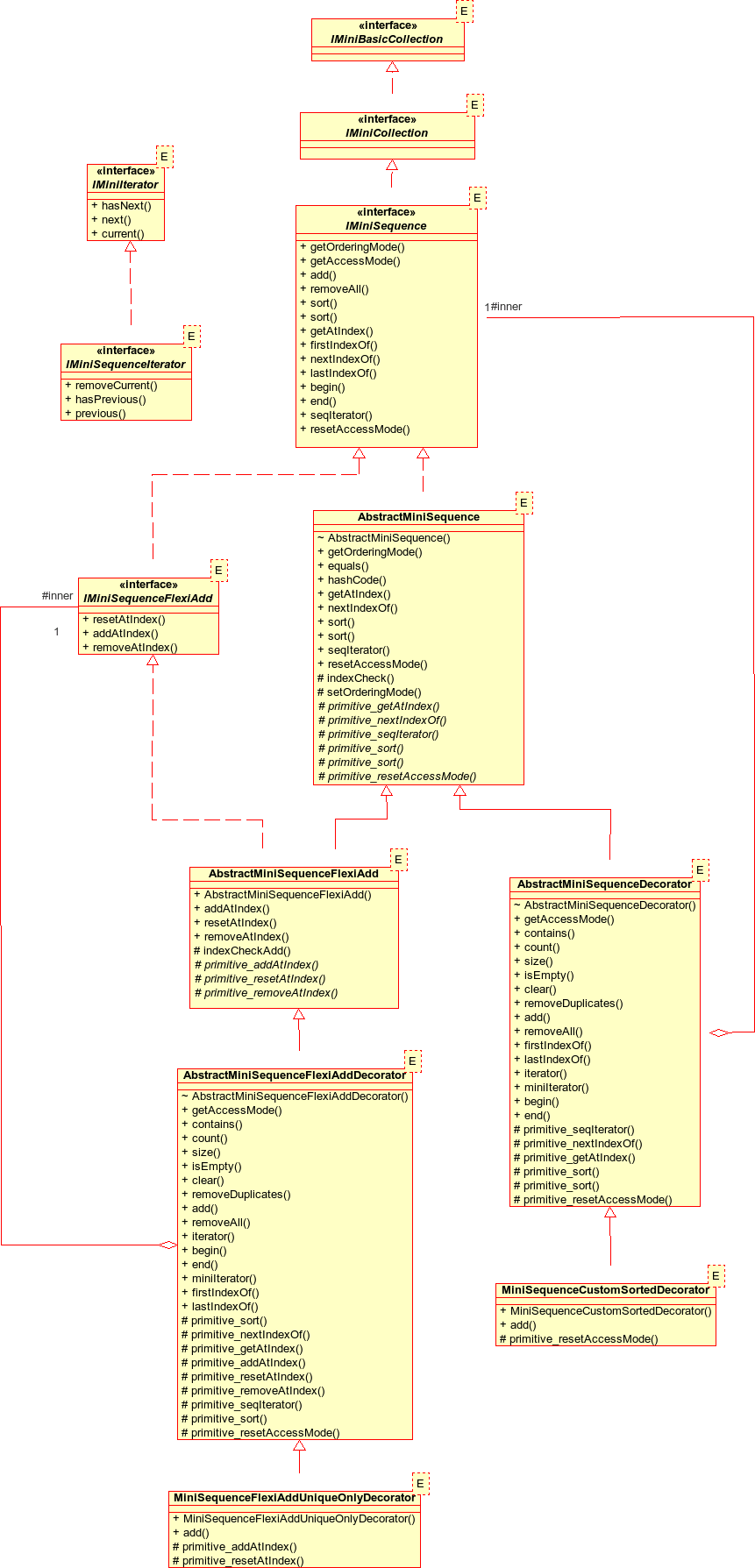
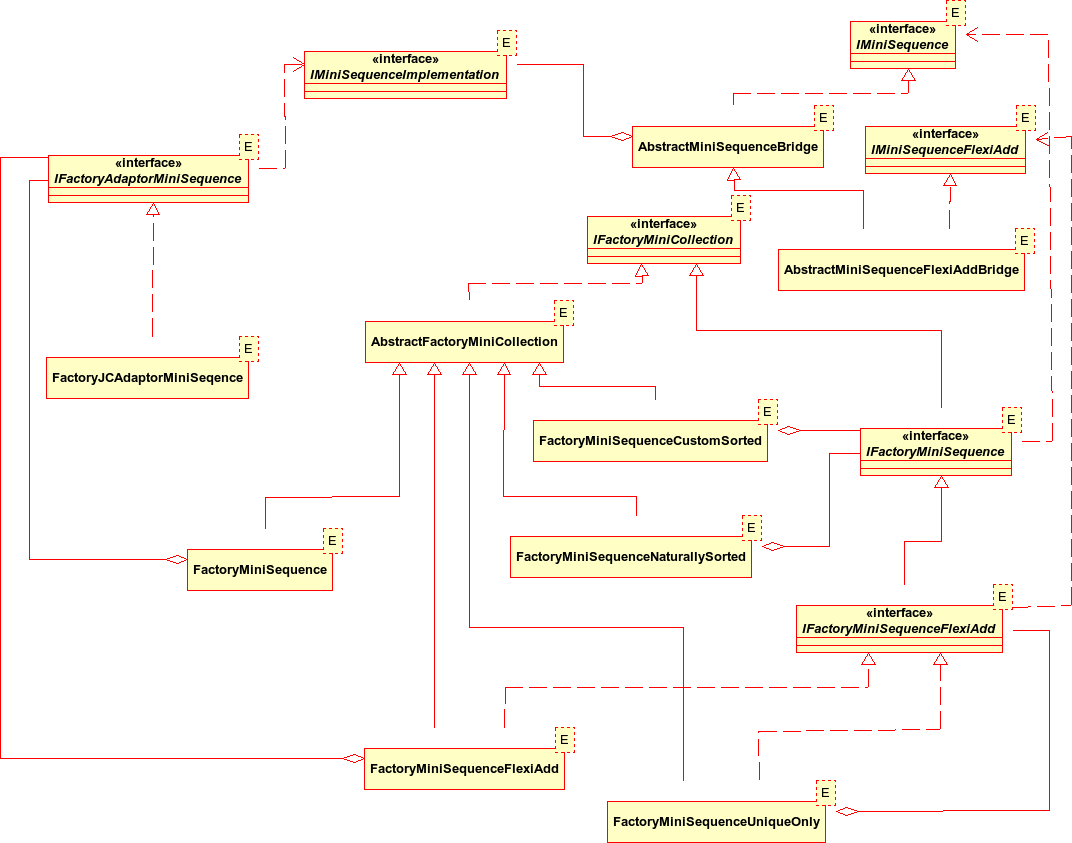
After adding the IMiniSequenceFlexiAdd type that allows addition, resetting and removal at specified index positions, and other improvements discussed in relation to the initial design detail, the design for sequences looks like this:

Sequences

IMiniSequence has an operation to reset the access mode (random access or sequential) which will ultimately be implemented by changing from one underlying container to another: this is facilitated in my design by the use of bridges.

AbstractMiniSequenceDecorator composes an IMiniSequence and is used in this design to provide the sorted sequences. Factories take responsibility for type checking and other details for naturally sorted sequences so we only need one concrete MiniSequenceCustomSortedDecorator and this adds sorting on add() and on a change in access mode (in case that causes a change in the order of the sequence).

The decorator adding unique-elements-only wraps an IMiniSequenceFlexiAdd type. IMiniSequenceFlexiAdd is a subtype of IMiniSequence. We can therefore use a factory to provide a uniques-only IMiniSequence (composing an IMiniSequence and returning an IMiniSequence type), as well being able to make uniques-only IMiniSequenceFlexiAdd sequences using this decorator. Using factories we can spare clients the need to have to know what they can wrap with what.

One problem I did encounter here was how to arrange the inheritance for the AbstractMiniSequenceFlexiAddDecorator. Ideally, I would not have had to replicate the operations in common with AbstractMiniSequenceDecorator, but I could not have AbstractMiniSequenceFlexiAddDecorator extending both AbstractMiniSequenceDecorator and AbstractMiniSequenceFlexiAdd. I thought about composing an AbstractMiniSequenceDecorator but as well as being complicated, this would either mean two copies of the composed sequence or AbstractMiniSequenceDecorator allowing AbstractMiniSequenceFlexiAddDecorator access to its inner sequence which was horrible. So I ended up by replicating the decorator operations. There is probably a nicer way to do this but I am not sure what it is.

Bridges and implementations

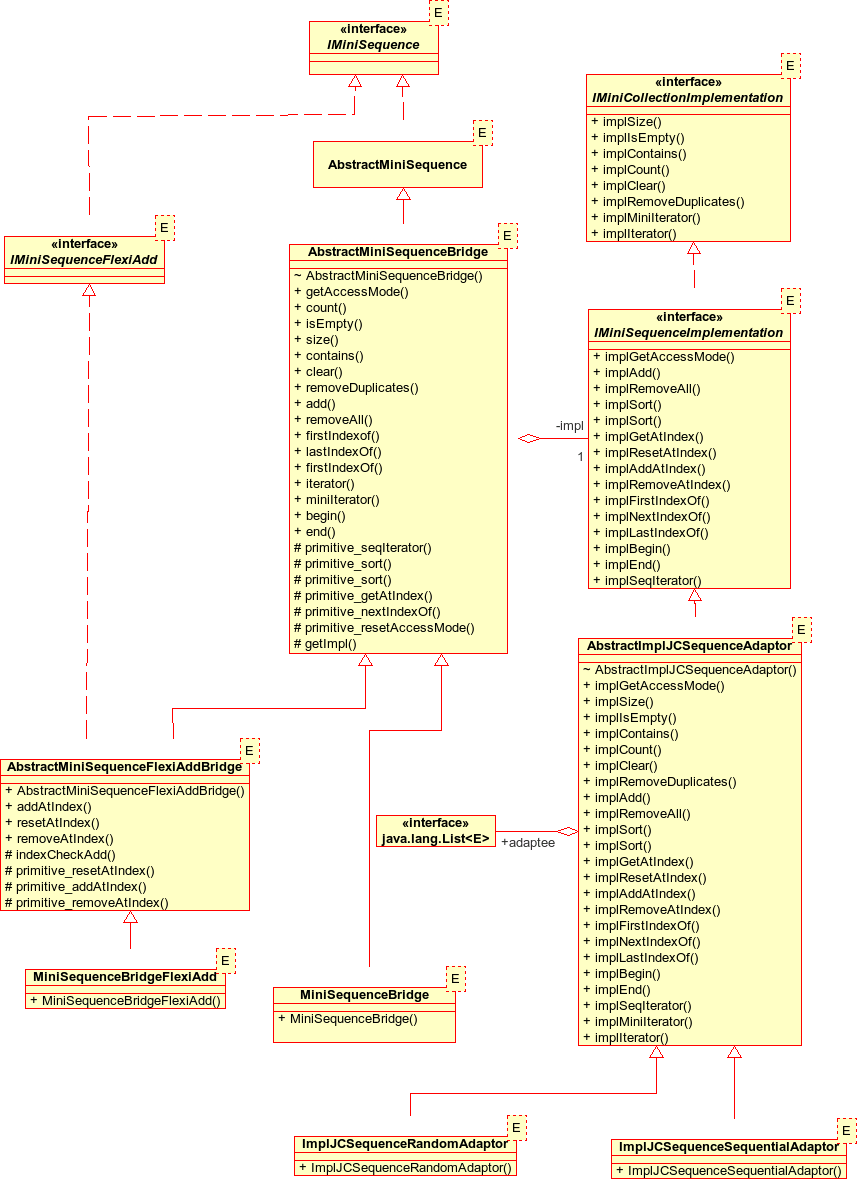
The final bridge and implementation design for sequences is shown below.

Sequence adaptors

The addition of the IMiniSequenceFlexiAdd type did not cause many problems for the bridges and implementations because I did not change the specification of the IMiniSequenceImplementation type: any implementation has to be able to provide an implementation for addAtIndex, resetAtIndex and removeAtIndex. The AbstractMiniSequenceBridge uses what it needs and is extended by AbstractMiniSequenceFlexiAddBridge which uses the remaining operations through a protected getter for the implementation (getImpl()). This worked for my small design and concrete implementations using adaptors of the Java List interface, but it does restrict what can be used as an implementation and means that AbstractMiniSequenceBridge is not using all the operations of its implementation. I am not very happy with this aspect of the design - I suspect that I was just tired of it by the time I got it working and did not want to have to think about it any more.

Iteration

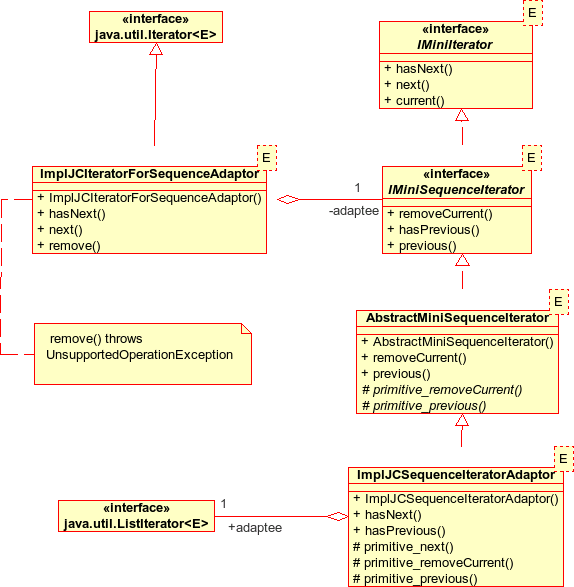
The IMiniSequenceIterator can remove the currently-pointed to element in the sequence and go backwards as well as forwards: other than the transfer of removeCurrent() from IMiniterator to the subtypes, the sequence iterator is essentially the same as in the initial design.

• the idiom for iterating through a sequence removing each element as you go with an IMiniSequenceIterator it is:

    (while it.current() != null) {
        it.removeCurrent();
        it.next();
    }

• or going backwards:

    (while it.current() != null) {
        it.removeCurrent();
        it.previous();
    }

For my sequence implementations I use adaptations of the Java ListIterator. I added an adaptation of my iterator back into the Java Iterator interface so that I could use the for-each construct. This was not strictly necessary for sequences - I could have just provided the Iterator on the adapted List, but I also wanted to nobble the Java Iterator remove() operation. I did this by taking shameless advantage of fact that Java regard remove() as 'optional'. I think that this is justified because implementing Iterable is not really part of the design, it is just to be able to show that we can use a for-each construct with the MiniCollection collections.

Bags of singles

Main types and classes

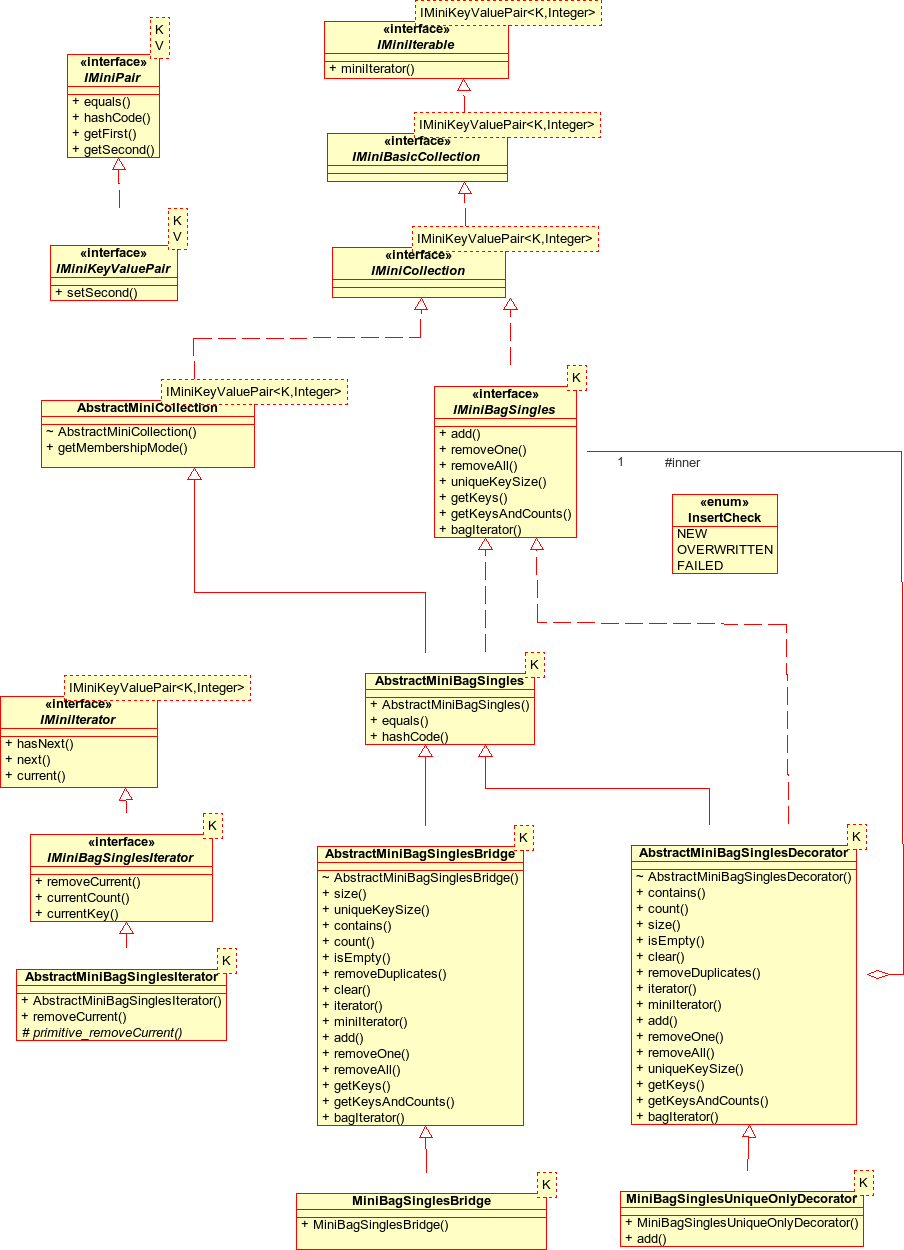
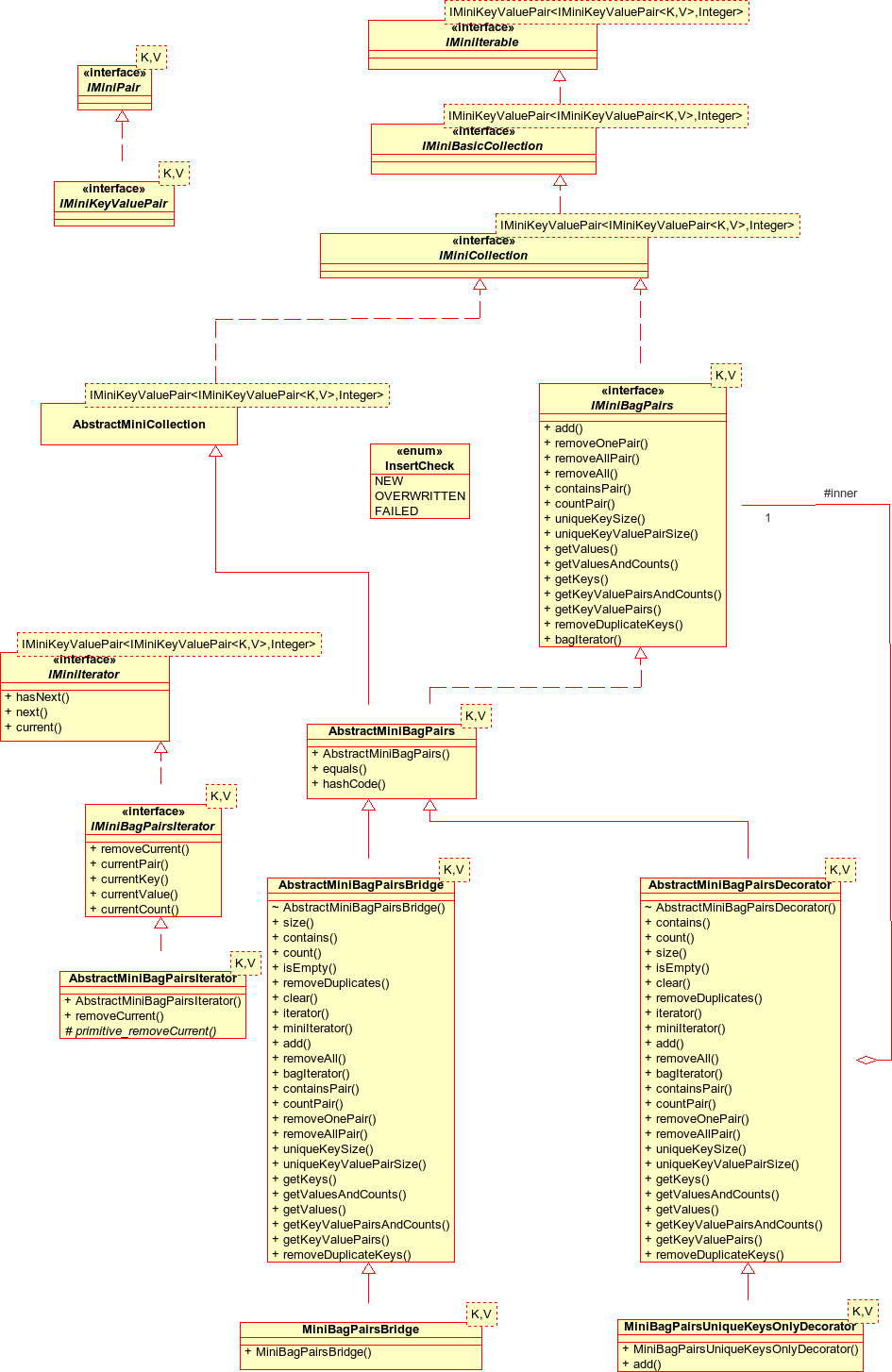
The generic type IMiniBagSingles is the subtype of IMiniCollection that represents a collection of objects with no ordering, parameterised with type K. In a sequence, duplicate copies of the 'same' object (ie comparing using equals()) are distinguished by their index position. In a bag, duplicate copies may exist but cannot be distinguished from each other. The collection can therefore be represented using (key, cardinality) pairs (represented with IMiniKeyValuePair types), where the cardinality is the number of copies of the key in the collection.

Bags of Singles

As an extension of IMiniCollection, IMiniBagSingles includes all the IMiniCollection operations. The size() operation returns the total number of keys in the bag, ie the sum over the unique keys of the number of copies of each unique keys. contains(K k) checks if the given key is in the bag, count(k k) returns the number of copies of the given key. clear() empties the bag, isEmpty() checks if the is empty. removeDuplicates() removes any duplicate copies of the keys so that the cardinality associated with each key is 1. The IMiniBagSingle operations are:

• Add keys to the bag using add(K k).
  • If the key is added as a new member of the bag then this operation returns an InsertCheck.NEW. If the operation resulted in an existing member being overwritten, the operation returns InsertCheck.OVERWRITTEN. If the operation fails because of the problem in the underlying implementation the operation can return InsertCheck.FAILED.
• Remove one copy of a specified key, or all copies of a specified key. If there is only one copy of the key in the bag, removeOne(K k) has the same result as removeAll(k k).
• Report the number of unique keys in the bag with uniqueKeySize() (size() returns the total number of keys, counting duplicate copies).
• Return a collection of the unique keys in the bag, or a collection of the (key,count) pairs. I have used IMiniSequences for return type.
• Return an IMiniBagSinglesIterator using the factory method bagIterator().

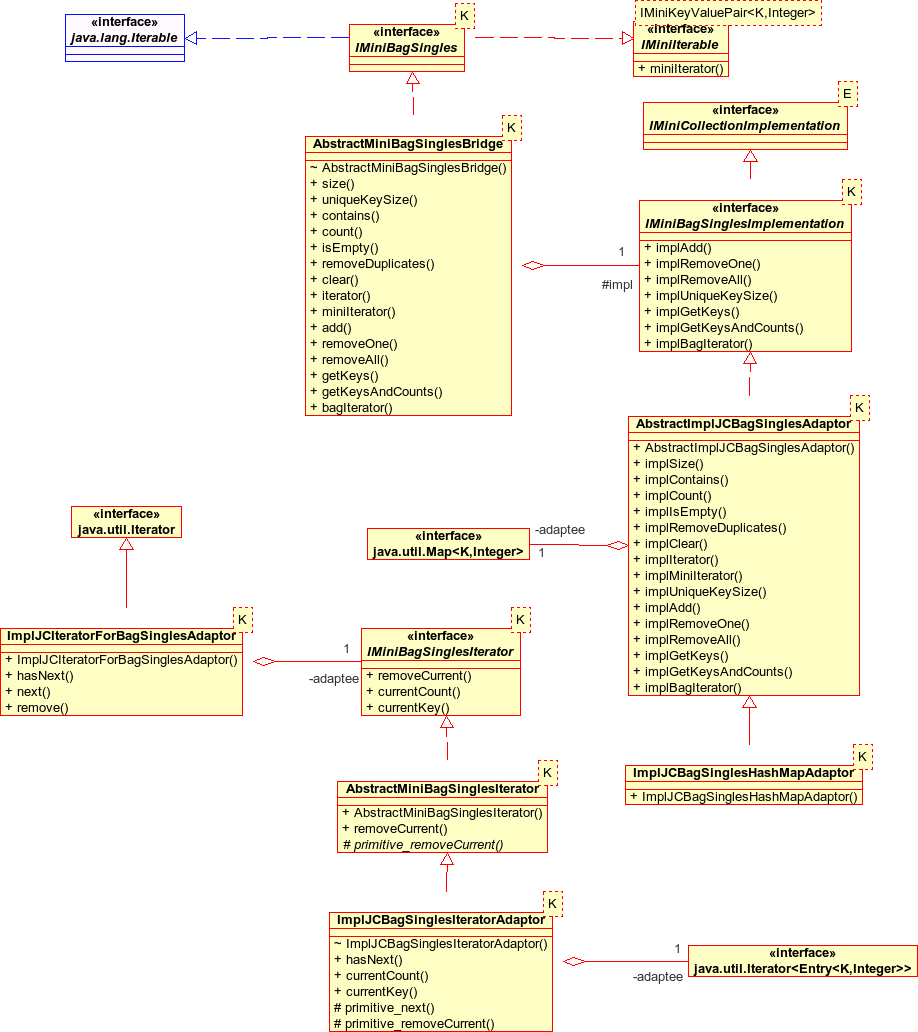
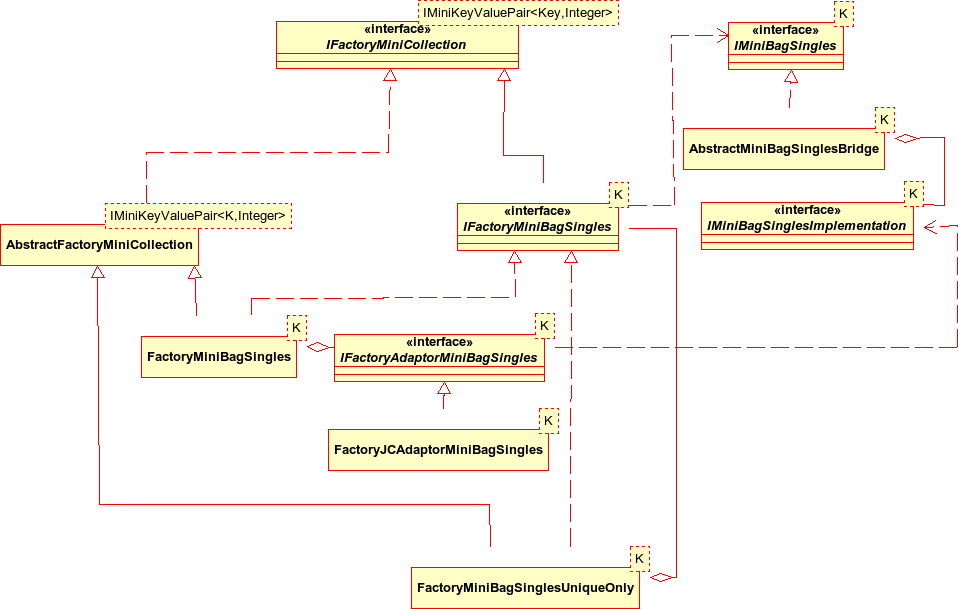
AbstractMiniBagSingles provides a stub abstract class for implementors to extend. As for sequences, my implementation is over a bridge.

I use the decorator pattern again to be able to have concrete subclasses adding variations to the IMiniBagSingles behaviour. AbstractMiniBagSinglesDecorator composes an IMiniBagSingles (noting the GoF stricture to keep the component class lightweight when using the decorator pattern).

MiniBagSinglesUniqueOnlyDecorator is the only concrete decorator in the design. The added behaviour is to remove existing members of the bag which compare equal to the new member after an add operation and thus ensure that there is only one copy of each unique key in the bag.

• add(K k) checks if the bag already contains a duplicate of the specified key and overwrites the existing copy if so. The post condition is that the specified key is added to the bag, and if there existed an element k' such that k.equals(k') == true then this has been overwritten and the operation has returned InsertCheck.OVERWRITTEN, else (no existing copy) the operation has returned InsertCheck.NEW.

Bridges and implementations

As with sequences, I wanted the flexibility to be able to use different bag implementations and to be able to change implementations dynamically if needed, so again I used a bridge pattern. AbstractMiniBagSinglesBridge composes an IMiniBagSinglesImplementation type and delegates its IMiniBagSingles operations to that implementation. The bridge does not have to know what concrete implementation it is using. IMiniBagSinglesImplementation extends IMiniCollectionImplementation: the combined interface has to mirror the IMiniBagSingles interface. One consequence of the bridge pattern that the GoF do not mention - probably because it's obvious to Real Programmers - is that it's better to work on the bridge only when the design of the abstraction you want to provide the implementation for is stable, or you end up having to make a lot of duplicate adjustments.

To get an implementation I adapt a Java Map to the IMiniBagSinglesImplementation interface, where the Map maps the key type K to Integer counts. To keep the flexibility to use adaptations of different Java Map subclasses I use an abstract object adaptor AbstractImplJCBagSinglesAdaptor which composes an instance of the Java Map adaptee type. The only concrete subclass I included will use a HashMap. The details of instantiation of the concrete bridge and concrete implementation adaptors are delegated to the factories.

Bag of Singles adaptors

Iteration

An IMiniIterator iterating over an IMiniBagSingles will iterate over the (key, cardinality) pairs in the bag (ie current() will return an IMiniKeyValue pair of key and cardinality, or null if the iterator does not point to any current pair). The IMiniBagSinglesIterator extends IMiniIterator to add operations to return the currentKey and currentCount separately, and be able to remove the current (key,cardinality) pair - equivalent to calling removeAll for the current key. IMiniBagSinglesIterator is implemented with ImplJCBagSinglesIteratorAdaptor by adapting a java.util.Iterator over the java.util.Set of Java.util.Map.Entry objects returned by the adaptee Map's entrySet() operation. The adaptation itself is clumsy and I am sure it could have been done better but I really just wanted to be able to use and test the design the the Bags of Singles. To get a java.util.Iterator type to return for the iterator() operation inherited from Iterable, and thus be able to for-each through the pairs in the bag, I adapted the IMiniBagSinglesIterator back to the Iterator interface, again using an object adaptor pattern. I could have used the java.util.Iterator over the java.util.Set of Java.util.Map.Entry objects again but I would still have have had to do the work converting the Map.Entry types into my IMiniKeyValue pairs so that the type used by the for-each construct is the same as the type for IMiniBagSinglesIterator.current(), so it was more interesting to adapt the IMiniBagSinglesIterator type. As with the for-each Iterator for sequences, my ImplJCIteratorForBagSinglesAdaptor does not implement remove().

Bags of pairs

Main types and classes

The generic type IMiniBagPairs is the subtype of IMiniCollection that represents a collection of associations between objects (key->value or (key,value) pairs), with no ordering within the bag of associations. Keys are parameterised as type K, values as type V. As with an IMiniBagSingles, duplicate copies of the same association ((key,value) pair) can be present, but are indistinguishable. The elements of the collection can therefore be represented using ((key,value), cardinality) pairs (pairs within pairs), where the cardinality is the number of copies of the association in the collection. The vanilla IMiniBagPairs type permits one key to map to multiple values and for multiple copies of that association to exist in the bag.

Bags of Pairs

IMiniBagPairs extends IMiniCollection. The size() operation returns the total number of (key, value) associations in the bag, ie the sum over the unique (key,value) associations of the number of copies of each unique association. contains(K k) checks if the given key is in the bag, count(K k) returns the number of associations for the given key. clear() empties the bag, isEmpty() checks if the is empty. removeDuplicates() removes any duplicate copies of the (key,value) pairs so that the cardinality associated with each pair is 1. The IMiniBagPairs operations are:

• Add key-value associations to the bag using add(K k, V v).
  • If the association is added as a new association in the bag then this operation returns an InsertCheck.NEW. If the operation resulted in an existing association being overwritten, the operation returns InsertCheck.OVERWRITTEN. If the operation fails because of the problem in the underlying implementation the operation can return InsertCheck.FAILED.
• Remove one copy of a specified key-value association, or all copies of a specified key-value association. If there is only one copy of the association in the bag, removeOnePair(K k, V v) has the same effect as removeAllPair(K k, V v).
• Remove all associations for a given key. If there is only one association for that key, removeAllPair(K k, V v) for that association has the same effect as RemoveAll(K k).
• check if the bag contains a specified key and value association with containsPair(K k, V v) or count the number of copies of an association with countPair(K k, V v).
• Report the number of unique keys in the bag with uniqueKeySize().
• Report the number of unique key-value pairs in the bag with uniqueKeyValuePairSize().
• Return a collection of the values associated with a specified key (getValues(K k)) or a collection of pairs of values and cardinalities with getValuesAndCounts(K k).
• Return a collection of the unique keys in the bag, or a collection of the unique (key,value) pairs, or a collection of the ((key, value), cardinality) pairs of pairs. I have used IMiniSequences for return type.
• removeDuplicateKeys() leaves each key with only one association to one value. The client cannot predict which association will be left in the bag and I am not sure if this operation should really be here: it could be used just to ensure that there is only one association in the bag for each key if you did not care which one is chosen.
• Return an IMiniBagPairsIterator using the factory method bagIterator().

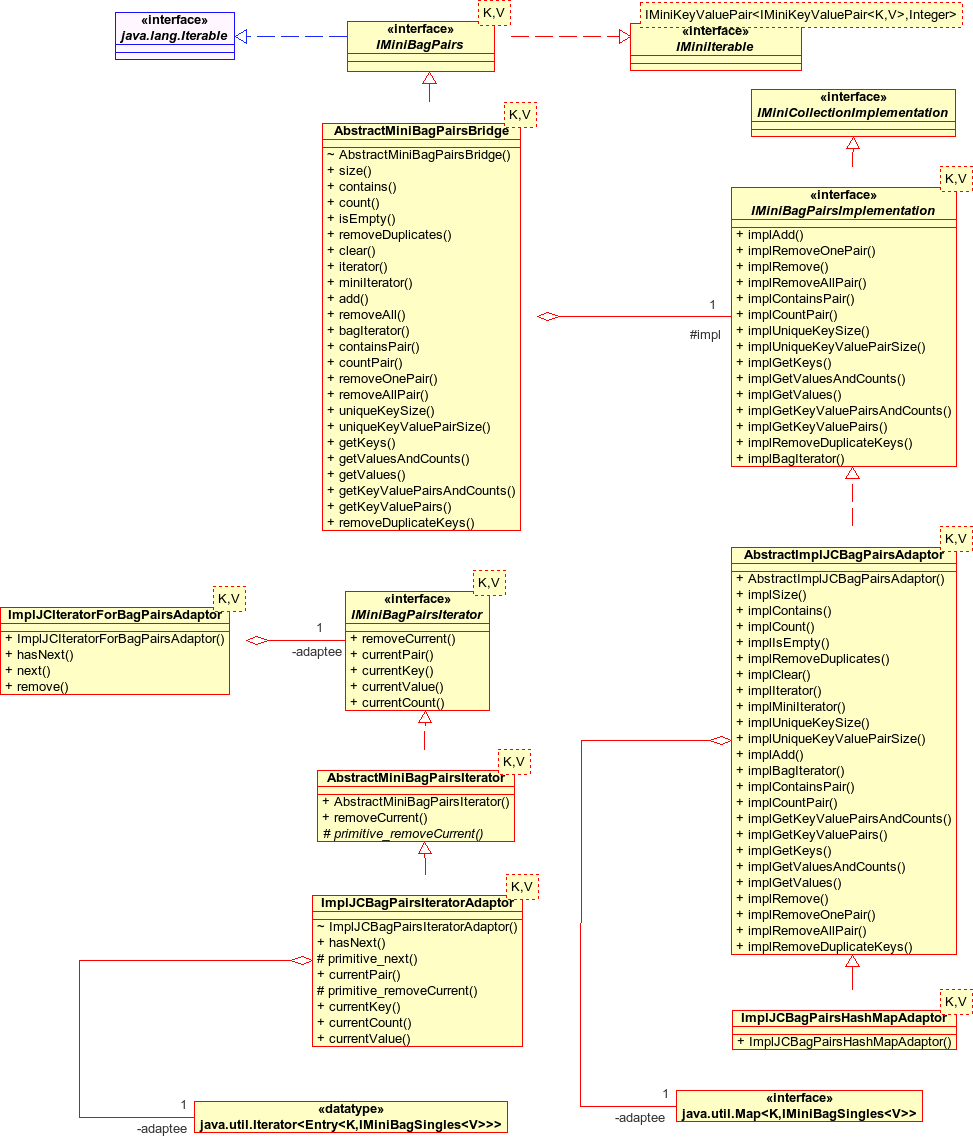
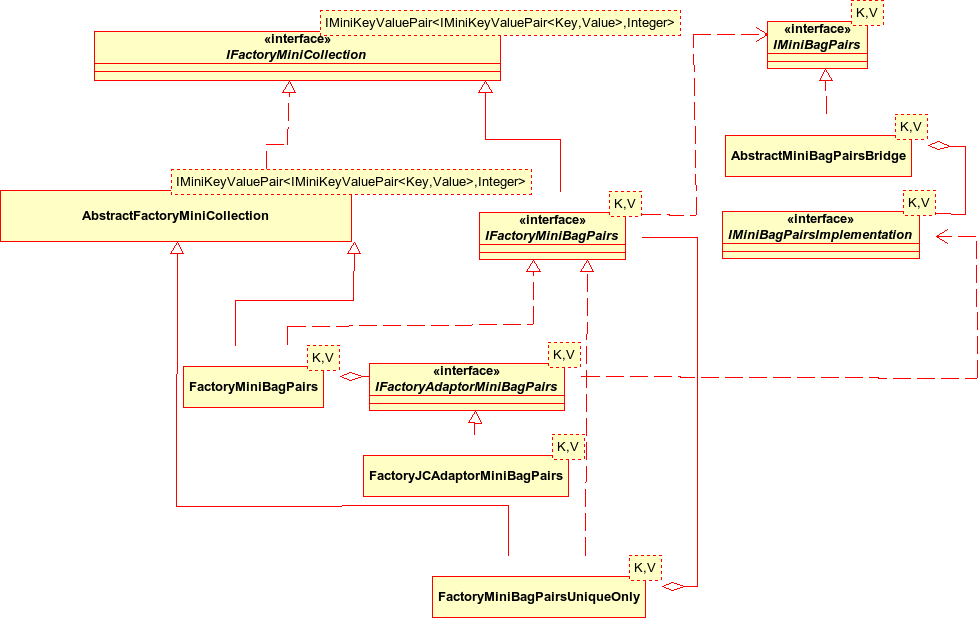
AbstractMiniBagPairs provides a stub abstract class for implementors to extend. As for sequences and bags of singles, my implementation is over a bridge.

I use the decorator pattern yet again to be able to add variations to the IMiniBagPairss behaviour. AbstractMiniBagPairsDecorator composes an IMiniBagPairs type.

MiniBagSinglesUniqueKeysOnlyDecorator is the only concrete decorator in the design. This provides the equivalent of the Java Map, allowing only one association for each key. The added behaviour is to remove any existing association in the bag where the key which compares equal to the key of the new association after an add operation and thus ensure that there is only one assocation for each unique key.

• add(K k, V v) checks if the bag already contains an association for the specified key k and overwrites the existing association with the new one if so. The post condition is that the specified key-value association is added to the bag, and if there existed an association with k' such that k.equals(k') == true then this has been overwritten and the operation has returned InsertCheck.OVERWRITTEN, else (no existing association) the operation has returned InsertCheck.NEW.

It would be straightforward to have a similar concrete decorator which allowed multiple associations for each key, but only one copy of each association.

Bridges and implementations

As with sequences and bags of singles, I wanted the flexibility to be able to use different bag implementations and to be able to change implementations dynamically if needed, so again I used a bridge pattern. AbstractMiniBagPairsBridge composes an IMiniBagPairsImplementation type and delegates its IMiniBagPairs operations to that implementation.

To get an implementation I adapt a Java Map to the IMiniBagPairsImplementation interface, where the Map maps the key type K to an IMiniBagSingles<V> collection, ie to a bag of pairs of values and cardinalities where the cardinality for a value is the number of times that the key associated with the bag of singles is associated with that value. This is similar to the common representation of multimaps as keys mapped to sets of values, except that IMiniBagPairs allows a key to be mapped to the same value more than once and this is reflected in the value, cardinality pairs in IMiniBagSingles collection associated with each key.

I use an abstract object adaptor AbstractImplJCBagPairsAdaptor, which composes an instance of the Java Map adaptee type, to allow me to use different Map implementations. The only concrete subclass I included will use a HashMap. The details of instantiation of the concrete bridge and concrete implementation adaptors are delegated to the factories, as usual.

Bag of Pairs adaptors

Iteration

An IMiniIterator iterating over an IMiniBagPairs will iterate over the ((key,value), cardinality) pairs of pairs in the bag. This type of current() is IMiniKeyValuePair<IMiniKeyValuePair<K,V>, Integer>, which is a bit of a mouthful for clients to disentangle. However, IMiniBagPairsIterator extends IMiniIterator to add operations to return the currentKey, currentValue and currentCount separately, and be able to remove the current ((key,pair), cardinality) pair of pairs from the bag - equivalent to calling removeAll for the current key. IMiniBagPairsIterator is implemented by ImplJCBagPairsIteratorAdaptor using a combination of a java.util.Iterator over the java.util.Set of Java.util.Map.Entry objects returned by the adaptee Map's entrySet() operation (which iterates over the K-IMiniBagSingles<V> pairs in the underlying hashmap) and an IMiniBagSinglesIterator over the contents of each IMiniSinglesBag. This achieves the desired result of ((key,value), cardinality) pairs of pairs as the return type for the iterator's current() operation. Again, the adaptation itself is messy and could have been done better. Because of the combination of the two different iterations, this is where it was particularly useful to adapt the IMiniBagPairsInterator into a java.util.Iterator type to return for the iterator() operation inherited from Iterable, and thus be able to for-each through the pairs of pairs in the bag and look like the for-each is using the IMiniBagPairsIterator. As with the for-each Iterator for sequences and bags of singles, my ImplJCIteratorForBagPairsAdaptor does not implement remove().

Abstract Factories

Clients instantiate the collections using abstract factories. The abstract factory pattern provides "an interface for creating families of related or dependent products without specifying their concrete classes" (Gof). It is particularly useful in this design because

• it allows us to control how the decorators are used (what can be decorated with what).
• the abstract factory can take care of the problem of how and when the implementations used by the bridges are created.

This design uses adaptor factories to make the implementation types used by the bridges. This decouples the bridges from how their implementations are instantiated while also keeping this hidden from the client. I have used separate abstract factories for each implementation type (IMiniSquenceImplementation, IMiniBagSinglesImplementation, IMiniBagPairsImplementation). Rather than creating a family of products with each concrete adaptor factory, the concrete factory really just creates one product type in different ways. The factory's construction operations replace the need for a variety of constructors in the implementations themselves. For example, a factory operation can take another collection as an argument and then the factory makes the new implementation using the concrete implementation's single constructor and takes care of transferring the contents of the collection into that new new implementation. I liked this because if I want to add a new way of making an implementation I add it to the factory rather than cluttering up the implementation class itself with lots of different constructors.

In the case of sequences, where there is more than one flavour of implementation available (random access, sequential access) the sequence adaptor factory uses parameterised operations to determine which access mode implementation to create. This has the disadvantage of giving a switch statement smell. With only two choices the switch statement is not large, but there were more flavours it would be come cumbersome (and each new flavour would necessitate editing all the operations using the parameter argument value switch). I think that this could be done more neatly even without getting rid of the parameterised operations entirely. The advantage of the parameterised operations in the adaptor factories is that the clients of these factories only have to know about a small number of operation signatures and possible parameter values to be able to make a wide range of products, rather than a very large number of different operation names.

The GoF discuss the disadvantages of parameterised factory operations in the context of ways to make abstract factories more extensible. The type-casting difficulties they mention are not relevant in this design because all the products do have the same type and it is the type expected by the client. They also suggest that the client "will not be able to differentiate or make safe assumptions about the class of product. If clients need to perform subclass-specific operations, they won't be accessible through the abstract interface". I consider that this is an acceptable disadvantage in this design. First, the interfaces are all the client needs to know about, there is no collection-related behaviour hidden in the subclasses. Secondly, I have provided the getAccessMode interrogation operation in the interface so that clients can check the access mode of the underlying implementation they are using.

In this design the clients of the adaptor factories are more factories - the factories to make the concrete collection types. There are abstract factories for each main type in the mini collections hierarchy: IMiniBasicCollection types (the fixed membership collection), IMiniSequence types, IMiniFlexiAddSequence types, IMiniBagSingles types and IMiniBagPairs types. Since all my concrete collections are bridges, each concrete collection factory needs to get hold of the required implementation, and it does this by composing an instance of the abstract adaptor factory type and asking this for the implementation. A concrete collection factory making bridges does have to know about the concrete implementation factories, but there is no coupling between the actual bridge classes and the concrete implementation classes or between the bridge factories and the concrete implementation classes. The bridge factories can also remain oblivious of different flavours of implementation by using parameterised operations for their 'make' commands and then just passing the parameters to the adaptor factory to sort out. Although the adaptor factories would have to be changed if more flavours were added, the collection factories would not.

I use different concrete collection factories for the main interface subtypes: each concrete decorator or permissable combination of decorators, for example has its own concrete factory. This has the disadvantage of (potentially) a large number of factories, but it also controls the way that decorators can be combined and means that adding a new decorator only means adding new factories, not altering existing ones. The factories for decorated collections compose instances of the factories for the inner, wrapped, collection and use these to create the component collection, so that each factory is as decoupled as possible from the business of the others.

Sequence factories

The collection factories can also provide compile-time type-checking where appropriate. For example, the snappily-named FactoryMiniSequenceNaturallySorted is parameterised with an <E extends Comparable<? super E>> type and the client will get a compile-time error if they try to instantiate this factory for an element type that does not implement Comparable. Once the type check is done, this factory just makes a Comparator class which uses E's compareTo method and passes this to a FactoryMiniSequenceCustomSorted factory, which in turn makes the decorators and asks its composed FactoryMiniSequence to make the inner sequence to wrap the decorator around.

Bag of Singles factories

Bag of Pairs factories